Derivation: Acceleration of the System

1. Equations of Motion

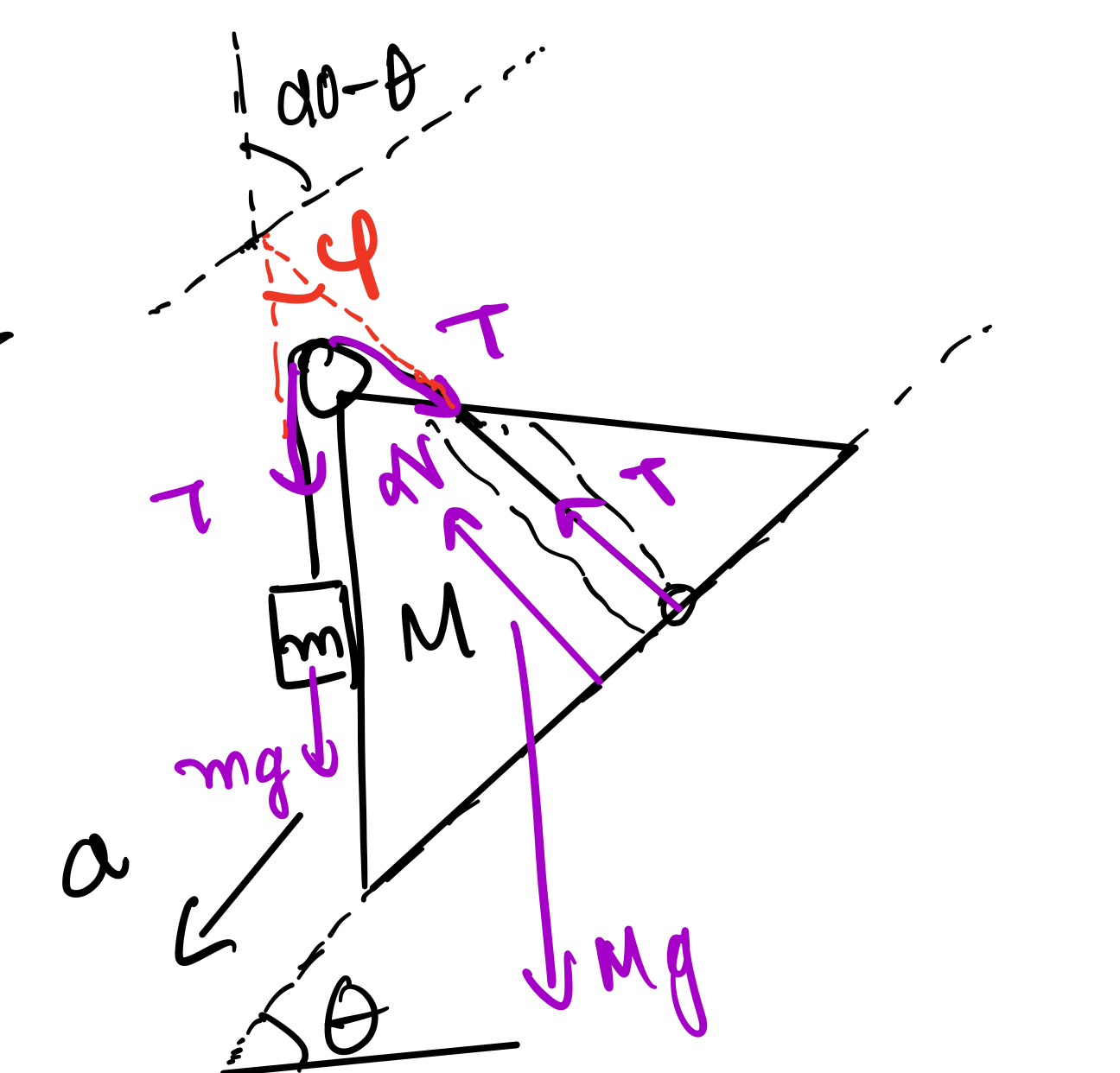
Considering the forces acting on the system along the incline and perpendicular to it:

(I) Equation along the incline (System):

$$ (m+M)g \sin\theta - \mu N - T \sin(\phi - \theta) = (m+M)a $$

(II) Normal Force Equation:

$$ N = (M+m)g \cos\theta + T \cos(\phi - \theta) $$

(III) Constraint Equation (Hanging Mass):

$$ mg - T = ma \sin\theta $$ $$ \Rightarrow T = m(g - a \sin\theta) $$

2. Substitution and Solving

Substitute the expression for $ N $ from (II) into (I):

$$ (m+M)g \sin\theta - \mu [(M+m)g \cos\theta + T \cos(\phi - \theta)] - T \sin(\phi - \theta) = (m+M)a $$

Rearranging to group terms associated with Tension $ T $:

$$ (m+M)g \sin\theta - \mu(m+M)g \cos\theta - T [\mu \cos(\phi - \theta) + \sin(\phi - \theta)] = (m+M)a $$

Note: Since the string is attached to a light ring, there shouldn't be any component of tension along the rod, so it should be perpendicular to the rod . This implies $ \phi = \theta $.
Therefore: $ \cos(\phi-\theta) = 1 $ and $ \sin(\phi-\theta) = 0 $.

The equation simplifies to:

$$ (m+M)g (\sin\theta - \mu \cos\theta) - \mu T = (m+M)a $$

Substitute $ T $ from (III) and solve for $ a $:

$$ a = \frac{g [ (m+M)(\sin\theta - \mu \cos\theta) - \mu m ]}{m + M - \mu m \sin\theta} $$

3. Final Result

Condition for motion ($ a > 0 $):

$$ \mu < \frac{(m+M)\sin\theta}{m + (m+M)\cos\theta} $$